Retomando los post anteriores, para determinar la calidad de los generadores de números aleatorios que nosotras elegimos (devC++, R, Geogebra y la calculadora) debemos comparar con la Distribución Uniforme (0,1) y analizar si cada conjunto de datos generados se aproxima a esta distribución y definir, si es posible a partir de la información que tenemos, cuál es el más aproximado.
Recordemos las características de la Distribución Uniforme Continua en el intervalo (a,b), a < b:
- Función de densidad de probabilidad:
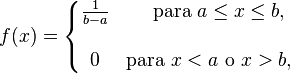
- Función de distribución:
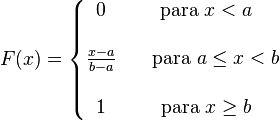
- Dominio:
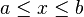
- Esperanza o media: E(X) =

- Varianza: V(X) =
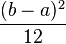
- Coeficiente de simetría: 0
- Coeficiente de curtosis: 9/5
Para este caso el intervalo queda definido por 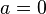 y
y 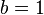 .
.
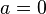 y
y 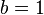 .
.
Entonces resulta:
 para
para 
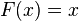 para
para 
A continuación presentamos las medidas de tendencia central y dispersión perteneciente a cada uno de los conjuntos de datos obtenidos, para compararlas con los valores teóricos. Pero, que estas medidas coincidan con los valores teóricos de la Distribución Uniforme (0,1) no nos asegura que las variables de los números generados tengan distribución similar a la Uniforme, para ello también necesitamos tener en cuenta los parámetros de forma (curtosis y asimetría).
Uniforme (0,1)
|
Datos de R
|
Datos C++
|
Datos Calculadora
|
Datos Geogebra
| |
Media
|
0.5
|
0.4730771
|
0.496885
|
0.47808
|
0.5008008
|
Desvío
|
0.2886751346
|
0.2981059
|
0.2854508
|
0.2864337
|
0.267806
|
Curtosis
|
-1.2
|
-1.284478
|
-1.13726
|
-1.179772
|
-0.8863847
|
Asimetria
|
0
|
0.09920876
|
-0.07215526
|
-0.0108821
|
-0.01843991
|
cuartil 0%
|
0
|
0.01394744
|
0.01919614
|
0
|
0.01008641
|
cuartil 25%
|
0.25
|
0.1840255
|
0.2600558
|
0.25475
|
0.3026029
|
cuartil 50%
|
0.5
|
0.4559388
|
0.5030366
|
0.463
|
0.520049
|
cuartil 75%
|
0.75
|
0.727682
|
0.7099445
|
0.73
|
0.7066047
|
cuartil 100%
|
1.00
|
0.9966363
|
0.9814447
|
0.986
|
0.9814372
|
N
|
100
|
100
|
100
|
100
| |
Figura 2: Medidas de tendencia central y dispersión, parámetros forma de cada una de las variables comparadas con los valores teóricos de la distribución Uniforme Continua (0,1).
Observando la Figura 2,vemos que los números arrojados se encuentran entre 0 y 0.9966363 como es de esperarse, además cada variable tiene su media y su desvío aproximado al del modelo uniforme. En este sentido podemos decir que la variable de los números generados con GeoGebra tiene la media más aproximada a 0.5 y el desvío de los números generados con la calculadora es el más aproximado a 0.28867. Para analizar con más detalle estas medidas, y poder tener una comparación visual, a continuación se presentarán los boxplot de cada una de las variables y de la uniforme (0,1).
Observando la Figura 2,vemos que los números arrojados se encuentran entre 0 y 0.9966363 como es de esperarse, además cada variable tiene su media y su desvío aproximado al del modelo uniforme. En este sentido podemos decir que la variable de los números generados con GeoGebra tiene la media más aproximada a 0.5 y el desvío de los números generados con la calculadora es el más aproximado a 0.28867. Para analizar con más detalle estas medidas, y poder tener una comparación visual, a continuación se presentarán los boxplot de cada una de las variables y de la uniforme (0,1).
También notamos que los parámetros de forma nos dan información bastante parecida a la deseada. Si la distribución es simétrica el coeficiente de asimetría debe ser cero, y en los casos de nuestras variables este coeficiente es aproximadamente cero. El coeficiente de curtosis debe ser -1.2, para nuestros casos es bastante próximo a -1.2, por lo tanto las variables tenidas en cuenta cuentan con una distribución platicúrtica (acumulan más valores en las colas, que la considerada estándar). Comparando los valores, la variable que tiene el coeficiente de curtosis más próximo a -1.2 es la de los números generados con la calculadora, la cual también tiene el coeficiente de asimetría más cercano a cero. Analizaremos con más detenimiento la forma de las distribuciones, en los gráficos de densidad que presentaremos más adelante.
La siguiente figura contiene los primeros cuatro BoxPlox correspondientes a las variables de números generados por la calculadora, DevC++, GeoGebra y R respectivamente y el último pertenece a una variable con distribución uniforme (0,1), para poder realizar la comparación deseada.
En cada Boxplot podemos observar el máximo, el mínimo y los cuartiles (0.25, 0.5 y 0.75). Los máximos y mínimos de cada Boxplot son muy próximos a 0 y 1, como también lo detallaba la Figura 2. Analizando los cuartiles, tanto desde el punto de vista numérico en la Figura 2, como los Boxplot de cada una de las variables, distinguimos que todas tienden a ser simétricas, acumulando aproximadamente el 25% hasta el primer cuartil, el 50% hasta el segundo y el 75% hasta el tercero, a excepción de la variable de números generados con R que el primer cuartil esta por debajo de 0.25 y los generados por GeoGebra que están por encima de 0.25. También podemos observar que la caja más parecida a la uniforme es la de la calculadora, pero ésta no cumple estrictamente con la simetría. La que es más simétrica es la caja de R, pero tiene un brazo más pequeño, lo cual nos habla de la poca dispersión de los datos entre el mínimo y el primer cuartil, y mayor dispersión entre el tercer cuartil y el máximo.
A continuación, mostraremos los histogramas de densidades para observar la forma que siguen cada una de las variables. De color negro marcamos la función de densidad de una distribución uniforme (0,1), esto nos ayudará a ver hasta dónde deberían ir las barras (correspondientes a los intervalos determinados por Sturges) de densidad de cada uno de los histogramas. En un primer momento, pensamos que los histogramas de GeoGebra y R tenían sus barras más próximas a la gráfica de la función de densidad, pero observando mas detenidamente, nos dimos cuenta que al tener valores muy extremos, los datos están muy dispersos en comparación al histograma de la calculadora, por ejemplo, que aunque no tengan la misma proporción, todos son cercanos a 1.
Todavía no podemos concluir cuál es el mejor generador, porque algunos se destacan por tener determinados valores más próximos a los del modelo uniforme, pero a su vez tienen otros que se alejan bastante. Lo que si debemos resaltar que, a diferencia de lo que habíamos supuesto, el generador de R no es, en primera instancia, el que se destaca del resto (no es el más parecido al modelo uniforme).
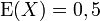

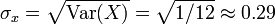













 respecto al cual se calculan los restos
respecto al cual se calculan los restos .
.